Оптимизация на търсенето в двоично търсещо дърво

Търсене в двоично търсещо дърво

Алгоритъмът за търсене на даден ключ в двоично търсещо дърво обикновено е следният:

Алгоритъм 1:

За търсене на ключ в двоично търсещо дъвро с корен върха :

1. Провери дали ключът е по-малък от ключа на корена . Ако е така, като резултат върни резултатът от търсене на ключ в лявото пъддърво на .

2. Провери дали ключът е по-голям от ключа на корена . Ако е така, като резултат върни резултатът от търсене на ключ в дясното пъддърво на .

3. Ако ключът на текущият възел съвпада с търсеният ключ , то върни като резултат h, иначе върни като резултат липса на елемент в дървото с даденият ключ.

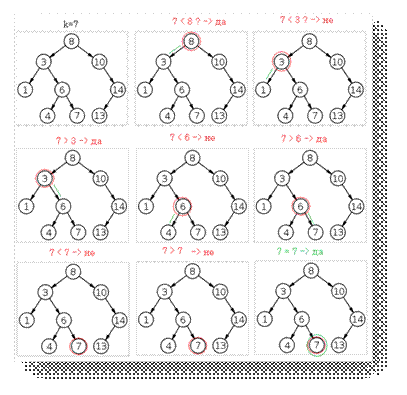
фиг.1. Илюстрация на търсене в двоично търсещо дърво

Примерен код 1 – C++

// binary tree sturcture

typedef struct node* link;

struct node{

int key;

link left, right;

};

//native search algorithm

link find(link h, int k){

if(h == NULL) return NULL;

if(k < h->key) return find(h->l, k);

if(k > h->key) return find(h->r, k);

return h;

}

Забележете, че в най-лошия случай горният алгоритъм извършва по две сравнения на възел от дървото. Когато сравненията са скъпи (например когато става въпрос за сравнение на стрингове), тези две сравнения по пътя водят до намаляване на ефективността на търсещото дърво.

Оптимизацията успява да осигури търсене в двоично търсещо дърво само с едно сравнение на възел, като постига това за сметка на константа допълнителна памет, използвана за указване на „най-близкия десен завой” по пътя към търсеният елемент:

Алгоритъм 2:

За търсене на ключ в двоично търсещо дъвро с корен върха :

1. Инициализация. Изпълнява се само един път през цялото търсене. Инициализирай глобален указател g към връх от двоичното търсещо дърво с нула.

2. Провери дали ключът е по-малък от ключа на корена . Ако е така, като резултат върни резултатът от търсене на ключ в лявото пъддърво на

3. Извърши присвояване g=h(направи g да сочи към текущият връх). Като резултът върни резултатът от търсене на ключ k в дясното поддърво на h.

4. Ако h е празен върх (без ключ), провери дали върхът, сочен от g има ключ k. Ако е така, върни като резултат g, имаче върни, че няма елемент със търсения ключ.

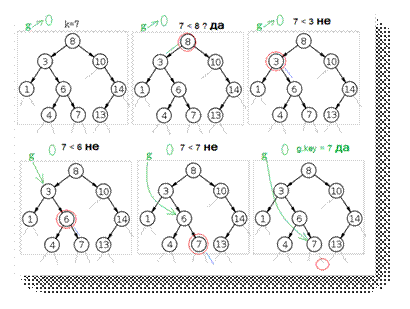
фиг.2. Илюстрация на търсене в двоично търсещо дърво с оптимизация

Примерен код 2 – C++

//optimised search algorithm

link g;

link find2(link h, int k){

g = NULL;

return find2_rec(h, k);

}

link find2_rec(link h, int k){

if(h == NULL){

if(g == NULL || g->key != k) return NULL;

else return g;

}

if(k < h->key) return find2_rec(h->l, k);

g = h;

return find2_rec(h->r, k);

}

Дори в простият пример от картинката се виждат спестените сравнения.

Литература

A. Andersson-A note on Searching in a Binary Search Tree. В статията може да намерите още информация за този метод и сравнителни тестове с други.